INTRODUCTION
Classification task is one of the fundamental problems in the field of machine learning. Among all kinds of methods, Support Vector Machine (SVM) plays an essential role. In this blog, I will give a mathematical derivation of SVM.
PROBLEM DESCRIPTION
The task of classification is that given a set of data points with different labels (e.g. red circles and green triangles shown in the figure below), looking for a decision boundary to separate this dataset. If the dataset is linear separable, we can always find a hyperplane to separate all data.
An existing challenge here is how to make the classifier capable to deal with unseen data. In other words, it means the classifier could be generalized well. From the perspective of SVM, it tries to maximize the fractional margin between data points and the hyperplane, as shown in the figure below.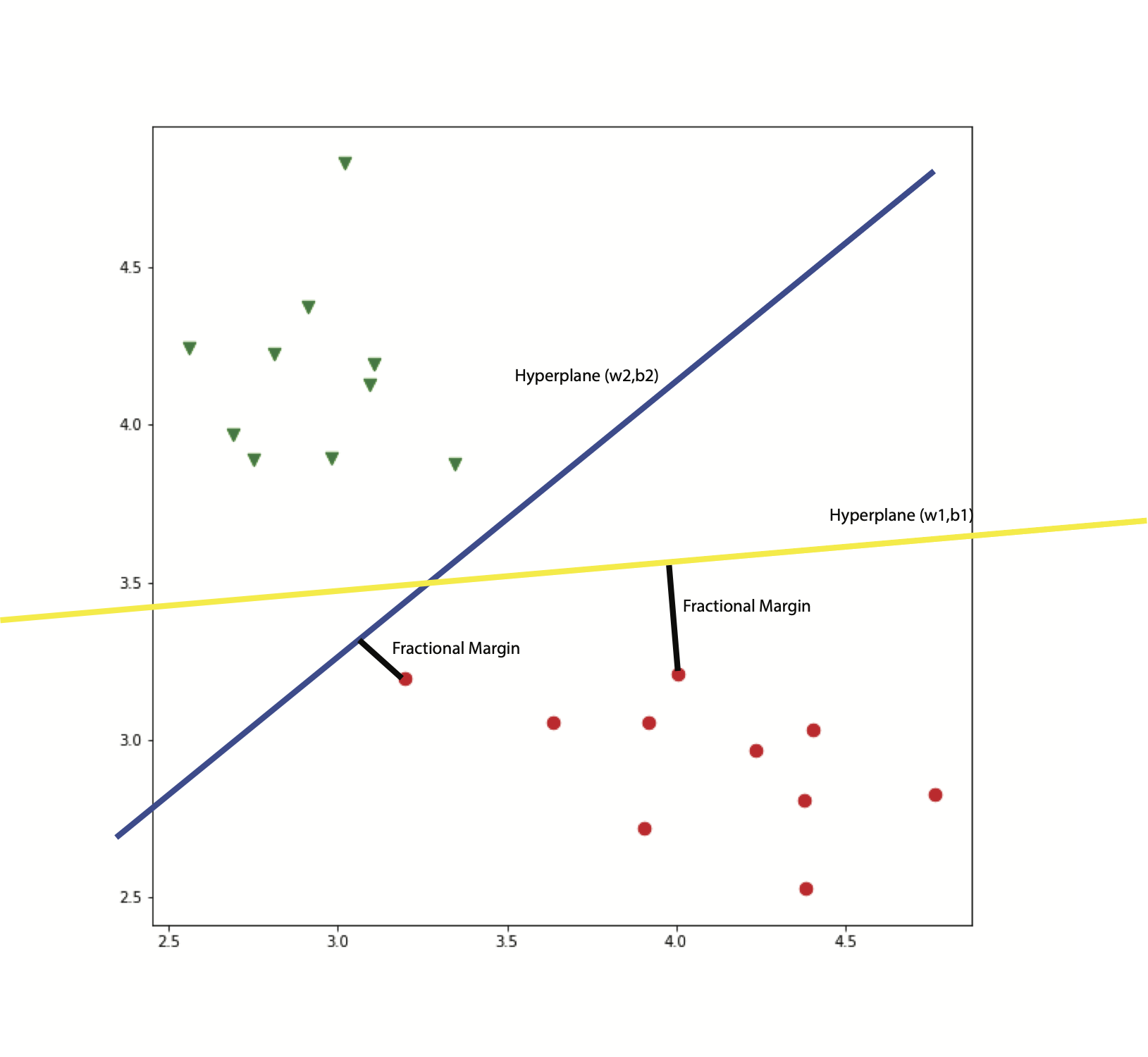
Given a set of data points ${x_{i},y_{i}}$, where $x_{i}$ is the feature vector and $y_{i}$ is the label (e.g. ${-1,1}$), the classifier is defined as:
$$h_{w,b}(x) = g(w^{T}x+b)$$
Where $g(z)$ is a sign function.
Then the fractional margin is:
$$\gamma_{i} = y_{i}(w^{T}x_{i}+b)$$
Here, we also define $\gamma = \min_{i} \gamma_{i}$. Thus the objective function for SVM is:
$$\max_{w, b, \gamma} \gamma$$
$$s.t. y_{i}(w^{T}x_{i}+b) \ge \gamma, \lVert w \rVert_{2}^{2}=1$$
The above objective function means we want to maximize the smallest the fractional margin.
DERIVATION
The original problem contains a non-convex constraint, meaning that there is no guarantee for the convergence of the optimization process. thus a variation of the original objective function is:
$$\max_{w, b, \gamma} \frac{\gamma}{\lVert w \rVert_{2}^{2}}$$
$$s.t. y_{i}(w^{T}x_{i}+b) \ge \gamma$$
In particular, the term $\frac{\gamma}{\lVert w \rVert_{2}^{2}}$ is also known as geometric margin. Now the constraints are convex but the objective function is still not convex yet. Then if we take a look at $\gamma$, we can impose another constraint here $\gamma = 1$. By doing this it does not really change the objective function, because the extract value of the fractional margin is scaled by the values of parameters of the hyperplane. By scaling, we can always make the minimum fractional margin equal to 1. Then we got the final version of the objective function here:
$$\min_{w, b} \frac{1}{2}\lVert w \rVert_{2}^{2}$$
$$s.t. y_{i}(w^{T}x_{i}+b) \ge 1$$
SOLUTION
A nice way to solve this problem is using the primal-dual algorithm. The origin problem is regarded as the primal problem. By taking the Lagrange multiplier method, we got:
$$L (w,b,\alpha) = \frac{1}{2}\lVert w \rVert_{2}^{2}+\sum_{i}\alpha_{i}(1-y_{i}(w^{T}x_{i}+b))$$
Here, we can define:
$$\theta_{p}(w,b) = \max_{\alpha, \alpha \ge 0} L(w, b, \alpha)$$
Then the primal problem is:
$$\min_{w,b} \theta_{p}(w,b) = \min_{w,b} \max_{\alpha, \alpha \ge 0} L(w, b, \alpha)$$
Accordingly, we can define:
$$\theta_{d}(\alpha) = \min_{w,b} L(w, b, \alpha)$$
then we can have our dual problem:
$$\max_{\alpha, \alpha \ge 0} \theta_{d}(\alpha) = \max_{\alpha, \alpha \ge 0} \min_{w,b} L(w, b, \alpha)$$
And dual problem provides a lower bound for the primal problem:
$$\min_{w,b} \max_{\alpha, \alpha \ge 0} L(w, b, \alpha) \ge \max_{\alpha, \alpha \ge 0} \min_{w,b} L(w, b, \alpha)$$
And the solution of the dual problem is also the solution of the primal problem when K.K.T. complementary conditions have been satisfied, which is:
$$\alpha_{i}(1-y_{i}(w^{T}x_{i}+b)) = 0$$
$$\frac{\partial L(w,b,\alpha)}{\partial w} = 0$$
$$\frac{\partial L(w,b,\alpha)}{\partial b} = 0$$
Here we got:
$$\frac{\partial L(w,b,\alpha)}{\partial w} = w-\sum_{i}\alpha_{i}y_{i}x_{i} = 0$$
$$\frac{\partial L(w,b,\alpha)}{\partial b} = -\sum_{i}\alpha_{i}y_{i} = 0$$
Plug the value of $w$ back to the Lagrange function:
$$L (\alpha) = -\frac{1}{2}\sum_{i}\sum_{j}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum_{i}\alpha_{i}$$
Following this, the dual problem is:
$$\max_{\alpha}L(\alpha)$$
$$s.t. \alpha \ge 0, \sum_{i}\alpha_{i}y_{i} = 0$$
After solving the $\alpha$, it could be plug back to get the value of $w,b$,
$$w = \sum_{i}\alpha_{i}y_{i}x_{i}$$
$$ b = -\frac{\min_{y_{i} = 1 } w^{T}x_{i} + \max_{y_{i} = -1 } w^{T}x_{i}}{2} $$
TAKE HOME QUESTION
HOW TO SOLVE $\alpha$?